Transformada de integrales

 T aplicada sobre la función f(x) de la forma siguiente:

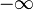La entrada de esta función T encontramos una función f(t), y la salida otra función F(u). Una transformada es un tipo especial de operador matemáti En ella t₁ y t₂ son dos valores que dependen de su definición, y pueden variar desde hasta .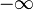

Hay numerosas transformadas integrales útiles. Cada una depende de la función K de dos variables escogida, llamada la función núcleo o kernel de la transformación.

Algunos núcleos tienen una K inversa asociada, K ^{− 1}(u,t) , que (más o menos) da una transformada inversa:

Un nucleo simétrico es el que es inalterado cuando las dos variables son permutadas.