Propiedades de laplace
Linealidad
Derivación
Integración
Dualidad
Desplazamiento de la frecuencia
Desplazamiento temporal
Nota: u(t) es la función escalón unitario
Desplazamiento potencia n-ésima
Convolución
Transformada de Laplace de una función con periodo p
Condiciones de convergencia
 (que crece más rápido que e − st) no pueden ser obtenidas por Laplace, ya que
(que crece más rápido que e − st) no pueden ser obtenidas por Laplace, ya que  , no es una función de orden exponencial de ángulos.
, no es una función de orden exponencial de ángulos.

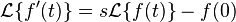

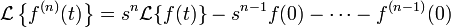




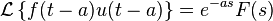

![\mathcal{L}\{\,t^nf(t)\} = (-1)^nD_s^n[F(s)]](http://upload.wikimedia.org/math/f/7/5/f75194212391d819688d6d298bd219d0.png)


No hay comentarios:
Publicar un comentario